RdRage - DIY HRNG for the security minded on a budget

In the wake of recent and not the recent events it became clear that weak pseudo random number generators are used to actively attack cryptographic systems. Besides that over the years there were incidents where insufficient gathering of seed material happend and PRNG implementations generated guessable random numbers after distro-specific source code changes for a cryptographic library. Additionally there were some controversy about new CPU instruction for a widly deployed cpu family that returns random numbers from the on-chip random number generator which unfortunately is a closed black box of magic.

Given these circumstances clearly an alternative true random number generator is needed. It not only should be secure, efficent and user-friendly but also within a reasonable price range and easy to aquire parts. The following documents my efforts to satisfy this requirements while pushing day-to-day computer security to new limits.

Hardware

Central part is the treasure chest which contains a hexagonal prism with pictograms on it: Ring, Flag, Scroll, Squid, Sword, Snake Pressing the trigger spins the prism and releasing it locks it in one then random position.

A hole was made into the bottom of chest and the top of the plastic box. The chest was glued on top of the box with the holes matching.

The webcam was quickly stripped of its housing, the LED sanded and then soldered onto the webcams PCB to eluminate the pictograms. This construction is secured inside plastic box.

Software

The softwaress logic is quite simple. It continously takes images from the webcam and performs pattern recognition to determine which symbol is facing the webcam. When it gathered three different states of the treasure chest it calculates an byte, outputs it and restarts this cycle.

Pattern Recognition

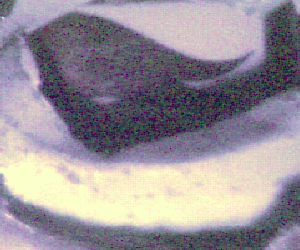
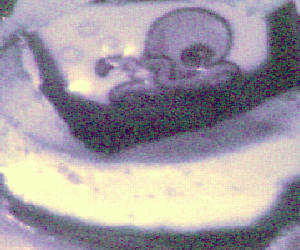
On startup the script initializes a table containing the filename of an reference image with a special value ranging from zero to five. After that for each reference the phash is calculated and stored in the same table.

The function getCurrent() takes a photo from the webcam calculates it phash. Then it measures the hamming distance to each of the reference images, the image with the smallest distance is choosen and its special value returned.

The most challenging part was to get a picture of the webcam, all commandline tools either segfaulted or returned ant sized distorted images. After hours of frustration I used kamerka a GUI-Tool from which it takes screenshots of the window via the X11 import function and crops them down. Obviously, for this to work the kamerka window needs to be the same dimension which is easy to achive by using an tiling window manager and starting everything in an fixed order.

	table = {'ring.png': Ref(0), 'scroll.png': Ref(1), 'sword.png':Ref(2), 'squid.png':Ref(3), 'snake.png':Ref(4), 'flag.png': Ref(5)}

	def getCurrent():
		a = sp.Popen("import -window Kamerka  test.png && convert test.png -crop 250x200+380+50 crop.png", shell=True, stdout=sp.PIPE, stderr=sp.PIPE)
		a.wait()

		target = pHash.imagehash("crop.png")
		h = 99999;
		n = 'undefined';

		for f1 in table:
			b = pHash.hamming_distance( target, table[f1].h)
			if b < h:
				h = b
				n = f1 

		return table[n].val

Number Generation

Detecting a spin is not trivial given that we don’t have a video feed or the possibility to read out the trigger state. Therefor we define a spin as “the current pictorgramm is not equal to the previous recorded”. After recording three stats these are combined to one “random byte”.

	a = 0
	b = 0
	c = 0

	while 1:
		a = getCurrent()
		while(a == c):
			a = getCurrent()

		b = getCurrent()
		while(b == a):
			b = getCurrent()


		c = getCurrent()
		while(c == b):
			c = getCurrent()

		rd_byte = (((a << 6) + b<< 3) + c) & 255
		print("%i" % rd_byte )

Analysis

The implementation obviously has two issues, the more obvious one is that for each random byte the adjacent states are disjunct. The second issue is that one states bit is cut of, which reduces the probability further. In theory an entropy source should be maximal, lets calculate the entropy of our random number generator.

First we calculate the possible variations for two (three bit)states: $ \frac{6!}{(6-2)!} = 30$ For the two bit state we have 4 variations but these have a non uniform distribution hence our distinction between the two and three bit states.

    0: 000       00
    1: 001       01
    2: 010   ->  10
    3: 011       11
    4: 100       00
    5: 101       01

Two variations have the probability $\frac{2}{6}$ and the other two have the probability $\frac{1}{6}$. With these informations we’re able to calculate the actual entropy:

$$ H(X) = - \sum_{x \in X} p_x \cdot \log_2(p_x) = -\left(\left( \frac{2}{6}\cdot\frac{1}{30} \cdot \log_2\left(\frac{2}{6}\cdot\frac{1}{30}\right)\right) \cdot 30 \cdot 2 + \left( \frac{1}{6}\cdot\frac{1}{30} \cdot \log_2\left(\frac{1}{6}\cdot\frac{1}{30}\right)\right) \cdot 30 \cdot 2\right)=6.835bit$$

$$\text{Loss: }8 - 6.835 = 1.165bit$$

If the last 3 bits of a byte from the RNG can be recovered the next byte can be guessed right with a probability of $\frac{1}{125}$ instead of $\frac{1}{256}$.

Seems alright.

Final remark

The attentive reader might have suspected something while reading. And indeed this HRNG is a result of an evening at a hackerspace driven by the whish to build something useful with the tad that was laying around. Clearly the HRNG should only be used for the matter of amusement at least until its validated by the FIPS 140 certification process which is still pending.